Written by Andrea Howard
on May 9, 2021

Multiple Imputation Madness

tl;dr summary:

If you use multiple imputation in Mplus software, you can’t request a single pooled asymptotic covariance matrix of the parameter estimates (at least not as of version 8.5). The output file containing separate covariance matrices for each iteration can’t be easily read into other software. Here I show how to read the file into R and how to get a pooled matrix, for later use in getting standard errors of point estimates and making plots and things.

love/hate

I like Mplus. A lot. It’s easy to use, it does (nearly) everything, and I know how to use it really well. But it’s also a bit fussy in some predictable ways and the times that I lose my temper with Mplus almost always involve multiple imputation (that thing you use all the time that works great? Sorry, not available with MI).

The other month I was working with a student who needed an asymptotic covariance matrix from Mplus (aka TECH3 output) to make some graphs of her fitted trajectories with confidence bands. If you’re hearing about asymptotic covariance matrices (or ACOV for short) for the first time, I’m talking about a matrix containing variances and covariances for each of the parameter estimates in a model. The diagonal elements of an ACOV matrix are the squared standard errors of each parameter estimate.

If you request TECH3 in Mplus, it will print in the output. If you want to export it to a separate file, you’ll get a fixed-width file containing the lower-triangular elements and diagonals of the ACOV matrix in free format (i.e., not arranged in rows and columns). Like so:

This particular model is a really simple linear growth curve so the ACOV matrix contains six variances for the six parameter estimates in this model: mean intercept, mean linear rate of change, variances for each of these, their covariance, and the residual (held equal across all repeated measures). The ACOV matrix also contains 15 unique covariances between all the parameter estimates. So altogether, I have 21 values in my TECH3 output.

Based on the instructions in the user’s guide, I know that the first value in TECH3 is the variance of the first parameter (which parameter is the “first” one? It’s the parameter with the number 1 attached to it in the Mplus TECH1 output). The second value is the covariance of the first and second parameter. The third value is the variance of the second parameter…and so on.

For a while now I’ve been very lazy and mostly doing simple stuff so I just copied and pasted the relevant values I needed from the ACOV matrix and put them somewhere I can use, like in a data table or matrix in R, or just literally building my own complete mini ACOV matrix in Excel and saving out the properly formatted table as a .csv file. What a pain.

Not too long ago another student I work with discovered the MplusAutomation package for R that is really slick at reading in various outputs from Mplus, including TECH3:

library(MplusAutomation)
myTECH3 <- readModels("mplusmodel.out", what = c("tech3"))

So if that’s all you need, you’re done here and no need to read on. But remember what I said earlier about all my Mplus troubles starting and ending with multiple imputation. The student I was helping had been running models with imputed data so she didn’t have just one TECH3 output to read… She had 100. And, predictably, Mplus does not create a pooled ACOV matrix for you, as far as I can tell. You just get 100 free-formatted lower triangular matrices stacked on top of each other. So now there’s a text file with 2100 values. Ordered? Yes. Easily usable? Not in a way that I could see, and the MplusAutomation package did not seem to have options for dealing with this.

100 TECH3 matrices

At this point I’m looking at two problems: (1) How do I get R (or any software really) to treat those 100 ACOV matrices as separate entities? And (2) Once I figure that out, how do I combine the relevant variances and covariances into a single pooled ACOV matrix that the student can use to make plots? After several false starts and expert advice from Kieran Healy via his data wrangling workshop, I settled on a relatively simple solution to the first problem.

First, instead of trying to read the data in elegantly as separate matrices, I just pulled all 2100 observations as a single numeric vector:

acov <- scan("acov.csv")

The file acov.csv was generated by Mplus after the student used the SAVEDATA command (e.g., SAVEDATA: TECH3 = acov.csv;)

Provided that you know how many elements are supposed to be in each covariance matrix, the split function can separate the large vector of numbers into a list of m vectors, where m is the number of imputations from your model. In my case, each matrix has 21 elements and there are m=100 total matrices:

elements <- split(acov, ceiling(seq_along(acov)/21))

Now I can access each of the vectors of 21 elements separately and use a for loop to rearrange the elements into their proper 6 x 6 matrices. I’ll start first by creating another list object called covmats that contains 100 empty 6 x 6 matrices:

covmats <- lapply(1:100, matrix, data=NA, nrow=6, ncol=6)

What’s going to happen in the loop is that we cycle through each empty matrix one by one and use a temporary matrix S to fill the upper triangle, including the diagonal, with the entries from the appropriate vector of elements. Then we use the upperTriangle and lowerTriangle functions from the gdata package to populate the lower triangle of each matrix and store the final result in our matrix list object covmats:

library(gdata)
for (i in 1:100){
  S <- covmats[[i]]
  S[upper.tri(S, diag=TRUE)] <- elements[[i]] 
  covmats[[i]] <- S
  lowerTriangle(covmats[[i]]) <- upperTriangle(S, byrow = TRUE)
}

I adapted this procedure from a really useful 10-year-old post on StackOverflow illustrating how to populate matrices in a related context.

If you print out one of the elements of covmats you should see something like this:

Once I can easily access the elements of each ACOV matrix (problem #1), I actually already know how to combine them across multiply imputed data using Rubin’s rules (problem #2).

one pooled ACOV matrix

What I need now is to read in the relevant parameter estimates from each of the 100 imputations. I don’t actually need to combine these myself, because Mplus has already done that in its own output, but I need each unique parameter estimate from each imputed file to pool the variances and covariances from the separate ACOV matrices. Here again, model results are stored in a single stacked file. Scrolling to the bottom of my Mplus output I see a legend showing me which items appear in what order in the file:

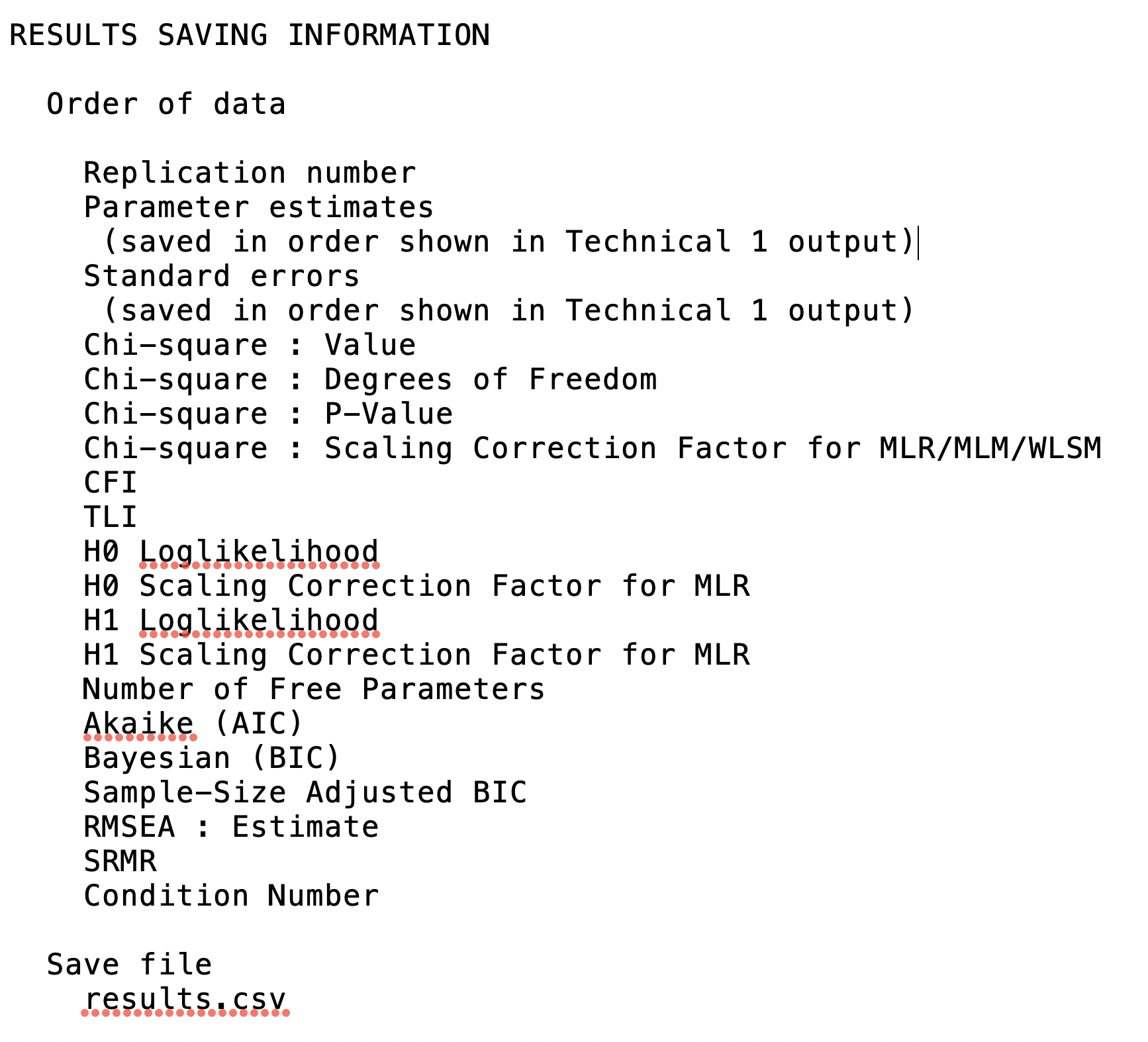
Ok, so the first entry tells me which imputed data file the results pertain to, and the next six entries will be the parameter estimates themselves.

results <- read.csv("results.csv", header=FALSE)

It turns out the programmers were purposeful about creating a row-column structure so every separate Thing from the above list given in the Mplus output starts on its own row. The Replication number appears on its own in the first row, the parameter estimates start on the second row, and so on:

and once I’ve read the data into R, it creates a data frame type object looking like this (showing just the output for the first imputed data file):

So as expected the first row contains just the “Replication number” (i.e., which imputation the results are from) and a bunch of NAs. The parameter estimates start in the second row. Given that this model has 6 parameter estimates, I can first make an empty matrix with 6 columns for the different parameter estimates and a row for each imputation (100 total).

params <- matrix(NA, nrow=100, ncol = 6)

Since each imputation takes up exactly 5 rows of data, I can anticipate that the parameter estimates in later iterations will start on the 7th, 12th, 17th, 22nd, and so on rows. If I make a sequence vector that starts at 2 and increments by 5, I can reference the correct row in results containing the parameter estimates from each imputation:

obs <- seq(from=2, by=5, length.out = 100)
> head(obs)
[1]  2  7 12 17 22 27

Now I can assign the parameter estimates from each imputation to its own row in the params matrix:

for (i in 1:100){
  params[i,] <- as.matrix(results[obs[i],1:6])
}

I’m finally ready to calculate the pooled asymptotic covariance matrix. Pooling variances across multiple imputations requires three steps, covered nicely in section 9.2 of Heymans and Eekhout’s 2019 online book on missing data analysis. Briefly:

Compute the within-imputation (co)variance portion by taking the mean of each element of the ACOV matrix over all 100 imputations. Recall that the individual ACOV matrices are stored in the list object covmats. I can use the Reduce function to calculate a mean for each element like so and store it in a pooled 6 x 6 matrix called varW:

varW <- Reduce('+',covmats)/length(covmats)

Compute the between-imputation (co)variance portion by calculating (co)variances for each parameter estimate over the 100 imputations. I’m going to need to do this in a for loop but first look at the key operation needed to make this happen:

varB <- (sum((params[ ,i]-mEst[i])*(params[ ,j]-mEst[j])))/99

For every element i in the params matrix (i.e., the parameter estimates), I need to subtract the mean over all 100 estimates to get a deviation score. I do the same thing for every element j in the params matrix, multiply the i and j deviation scores together and add them up. When i = j, you get a sum of squares. When i ≠ j, you get a sum of cross-products. Dividing by the number of imputations minus 1 (100-1 or 99 in this case) gives a variance (when i = j) or a covariance (when i ≠ j).

Compute total (co)variance using the following formula:

varW + varB + (varB/m)

Here’s the complete loop for performing all three of these steps:

varW <- Reduce('+',covmats)/length(covmats)
mEst <- matrix(NA)
seEst <- matrix(NA, nrow=6,ncol=6)
for (i in 1:6){
  for (j in 1:6){
  mEst[i] <- mean(params[ ,i])
  mEst[j] <- mean(params[ ,j])
  varB <- (sum((params[ ,i]-mEst[i])*(params[ ,j]-mEst[j])))/99
  seEst[i,j] <- varW[i,j] + varB + (varB/100)
}}

And that’s it. The object seEst contains the pooled ACOV matrix:

I checked to make sure I hadn’t made any dramatic errors by taking the square roots of the diagonal elements and checking them against the pooled standard errors from the original Mplus output. Below I show this in a pipeline, but you’ll minimally need to load the magrittr package or at least one tidyverse package to access the pipe %>% function:

library(magrittr)
seEst %>% 
  diag() %>% 
  sqrt() %>% 
  round(3)

# output from the console:
[1] 0.043 0.079 0.017 0.106 0.016 0.005

Here are the relevant bits of original output from Mplus so you can check that the standard errors are correct:

MODEL RESULTS
                                                    
                    Estimate       S.E.   

! Parameter #5
 I        WITH
    S                 -0.004      0.016     

! Parameters #2 and #3
 Means
    I                  3.165      0.079     
    S                  0.022      0.017    

! Parameters #4 and #6
 Variances
    I                  0.571      0.106    
    S                  0.002      0.005    

! Parameter #1
 Residual Variances
    y1                 0.329      0.043    
    y2                 0.329      0.043    
    y3                 0.329      0.043    
    y4                 0.329      0.043    
    y5                 0.329      0.043

one last thing

I actually only need the elements of the ACOV matrix that contain the variances and covariance for the two fixed effects in the model: the mean intercept and slope. The TECH1 output from Mplus told me that these estimates are elements 2 and 3 in TECH3, so I can make a reduced ACOV matrix containing just these (co)variances:

reduced <- seEst[c(2,3),c(2,3)]

Once you have your ACOV matrix and you want to use it to make some great plots of your longitudinal data but don’t know how, I made a couple of long videos (sorry) for plotting raw data and fitted data when my workshop appearance at a conference in 2020 got COVID-cancelled.

If after skimming through you this happen to be someone who knows a five-second alternative to doing all this work, great. Email or find me on Twitter and I’ll happily add a postscript here pointing folks in the right direction.

Top